Probabilistic
Analysis using a Theorem Prover
Time: August 2, 2009 (Morning Session)
Location: McGill University, Montreal,
Canada
Organizers: Osman
Hasan and Sofiene Tahar
Organizer Affiliation: Department
of Electrical and Computer Engineering, Concordia University, Montreal,
Canada
Summary
Hardware and software systems usually exhibit some random
or unpredictable elements. Examples include failures due to environmental
conditions or aging phenomena in hardware components and the execution of
certain actions based on a probabilistic choice in randomized algorithms.
Moreover, these systems act upon and within complex environments that themselves
have certain elements of unpredictability, such as noise effects in hardware
components and the unpredictable traffic pattern in the case of telecommunication
protocols. Due to these random components, establishing the correctness of
a system under all circumstances usually becomes impractically expensive.
The engineering approach to analyze a system with these kind of unavoidable
elements of randomness and uncertainty is to use probabilistic analysis. Even
for hardware and software systems for which correctness may be unconditionally
guaranteed, the study of system performance primarily relies on probabilistic
analysis. In fact, the term system performance commonly refers to the average
time required by a system to perform a given task, such as the average runtime
of a computational algorithm or the average message delay of a telecommunication
protocol. These averages can be computed, based on a probabilistic analysis
approach, by using appropriate random variables to model inputs for the system
model. Traditionally, computer simulation techniques are used to perform probabilistic
analysis. However, they provide less accurate results and cannot handle large-scale
problems due to their enormous computer processing time requirements. This
unreliable nature of the results poses a serious problem in safety critical
applications, such as those in space travel, military, and medicine. A possible
solution for overcoming these limitations is to conduct probabilistic analysis
within the sound core of a higher-order-logic theorem prover. Due to the
high expressiveness of the higher-order logic and the inherent soundness
of interactive theorem proving, this approach can be used to conduct error
free probabilistic analysis of any system, which can be expressed mathematically,
at the cost of significant user interaction.
There have been some recent developments related to the
automated reasoning of probabilistic notions, such as the formalization of
both discrete [1] and continuous [2,3] random variables in higher-order-logic
and the verification of their corresponding probabilistic [4] and statistical
properties [5,6,7] in a theorem prover. We believe that by utilizing these
capabilities, we can handle the higher-order-logic theorem proving based probabilistic
analysis of a variety of hardware and software systems with reasonable amount
of modeling and verification efforts. The main idea, illustrated in the figure
below, is to construct higher-order-logic models of systems while representing
their random components by appropriate formalized discrete and continuous
random variables. The probabilistic and statistical characteristics of the
system can then be formally reasoned about in a theorem prover using the
probability distribution functions, such as probability mass function (PMF)
and cumulative distribution function (CDF), and statistical quantities, like
mean and variance, of the random variables used in its model.
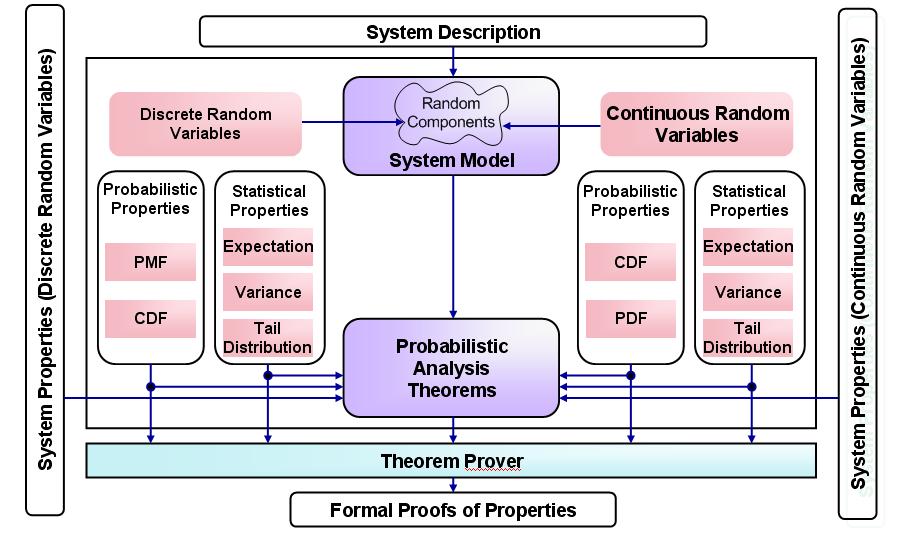
The above infrastructure has been successfully used for
the analysis of the Coupon Collector's problem [7], the automated repeat request
(ARQ) communication protocols [8], the Stop-and-Wait protocol [9], the ARQ
mechanism at the logic link control (LLC) layer of the General Packet Radio
Service (GPRS) [10] and the repairability condition of hardware reconfigurable
memory arrays in the presence of stuck-at faults [11]. The main focus of the
tutorial is to introduce the above mentioned higher-order-logic formalizations
of probability theory concepts and present their practical effectiveness for
conducting precise probabilistic analysis of real world hardware and software
systems. The tutorial is organized as follows:
- Introduction
- Motivation
- System Verification
- Probabilistic Analysis
- Simulation: State-of-the-art Probabilistic Analysis Approach
- Probabilistic Model Checking
- Higher-order-logic Theorem Proving and HOL
- Probabilistic Theorem Proving
- Formalization of Discrete Random Variables
- Verification of Probability Mass Functions (PMFs)
- Formalization of Continuous Random Variables
- Formalization of Cumulative Distribution Functions (CDFs)
- Formal Verification of Statistical Properties
- Case Studies
- Probabilistic Analysis of Coupon Collector's Problem
- (A commercially used algorithm)
- Average Message Delay relation for the Alternating-Bit Protocol
- (A classical real-time communication system
- Repairability of Reconfigurable Memory Arrays in the presence of
Stuck-at and Coupling Faults
- (A hardware reliability issue)
- Conclusions and Future Directions
Contact
Osman Hasan: o_hasan AT ece DOT concordia DOT ca
Sofiene Tahar: tahar AT ece DOT concordia DOT ca
References
[1] J. Hurd.
Formal Verification
of Probabilistic Algorithms. PhD Thesis, University of Cambridge, Cambridge,
UK, 2002.
[2]
O.Hasan and
S. Tahar. Formalization
of the Standard Uniform Random Variable. Theoretical Computer Science, Vol.
382, No. 1, Elsevier B.V. Pub., 2007, pages 71-83.
[3] O.
Hasan and S.
Tahar:
Formalization
of Continuous Probability Distributions; In: F.
Pfenning (Ed.
), Automated
Deduction, Lecture Notes in Computer Science 4603, Springer
Verlag, 2007, pp. 2-18. [
Proc. 21st Conference
on Automated Deduction (CADE-21),
Bremen, Germany,
July 2007.]
[4] O.
Hasan and S.
Tahar:
Verification
of Probabilistic Properties in the HOL Theorem Prover;
In: J. Davies and J. Gibbons (Eds.),
Integrated Formal Methods,
Lecture Notes in Computer Science 4591, Springer
Verlag, 2007, pp. 333-352. [
Proc. International
Conference on Integrated Formal Methods (IFM'07),
Oxford, UK, July 2007.]
[5] O.
Hasan and S.
Tahar:
Verification
of Expectation Properties for Discrete Random Variables in HOL; In:
K.Schneider and
J.Brandt
(Eds.),
Theorem Proving in Higher-Order Logics, Lecture Notes
in Computer Science 4732, Springer
Verlag,
2007, pp. 119-134. [
Proc. International Conference on Theorem Proving
in Higher-Order Logics (TPHOLs'07),
Kaiserslautern, Germany,
September 2007.]
[6]
O.Hasan and
S. Tahar. Using Theorem Proving
to Verify Expectation and Variance for Discrete Random Variables.
Journal
of Automated Reasoning, Springer Verlag, Vol. 41, No. 3-4, Springer
Verlag, November 2008, pp. 295-323.
[7]
O.Hasan and
S. Tahar. Formal
Verification of Tail Distribution Bounds in the HOL Theorem Prover. Mathematical Methods in the Applied
Sciences, Wiley InterScience, Vol.
32, no. 4, Wiley Interscience, March 2009, pp. 480-504.
[8] O.
Hasan and S.
Tahar:
Performance
Analysis of ARQ Protocols using a Theorem Prover;
In
IEEE International Symposium on Performance Analysis of Systems
and Software (ISPASS'08), IEEE Computer Society, Austin, Texas, USA,
April 2008, pp. 85-94.
[9]
O.Hasan and
S. Tahar. Performance Analysis
and Functional Verification of the Stop-and-Wait Protocol in HOL.
Journal
of Automated Reasoning, Springer Verlag, Vol. 42, No. 1, Springer
Verlag, January 2009, pp. 1-33.
[10]
O. Hasan and S. Tahar:
Performance
Analysis of Wireless Systems using Theorem Proving; In: Jens Chr. Godskesen
and Massimo Merro (Eds.), First International Workshop on Formal Methods
for Wireless Systems (FMWS'2008), Toronto, ON, Canada, August 2008,
pp. 3-18, ISSN 1600-6100, ISBN 978-87-7949-183-0.
[11]
O. Hasan, N. Abbasi and S. Tahar:
Formal
Probabilistic Analysis of Stuck-at Faults in Reconfigurable Memory Arrays;
In: M. Leuschel and H. Wehrheim (Eds.),
Integrated Formal Methods,
Lecture Notes in Computer Science 5423, Springer
Verlag,
2009, pp. 277-291. [
Proc. International Conference on Integrated
Formal Methods (IFM'09), Düsseldorf, Germany
, February 2009.]
Last Updated: July 9, 2009.


