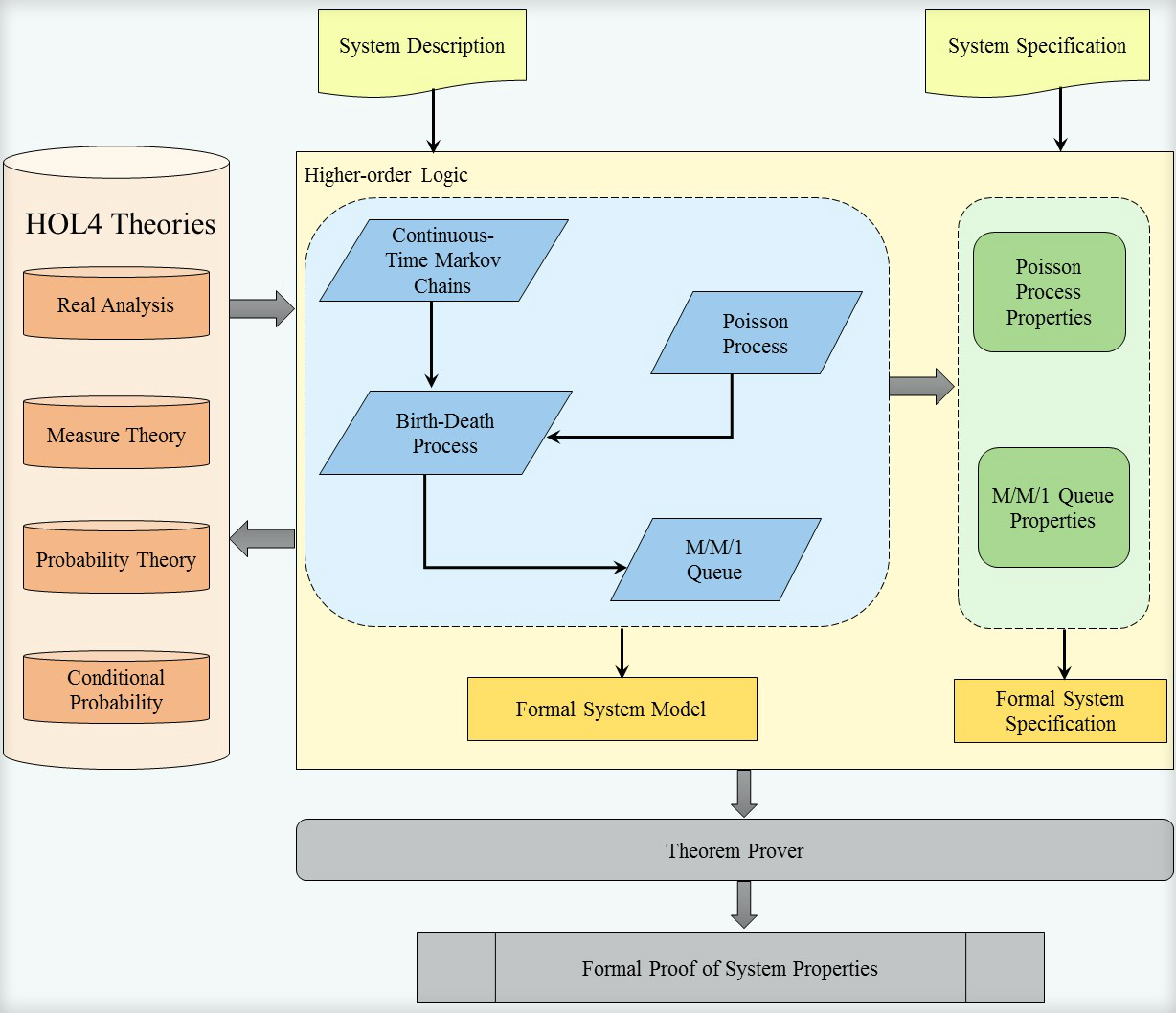
The performance analysis of engineering systems have become very critical due to their usage in safety and mission critical domains such as military and biomedical devices. Such an analysis is often carried out based on queuing theory which involves Markov Chains with continuous time behavior. In this research project, we propose to use higher-order-logic theorem proving as a complementary approach to simulation and computer algebra systems to conduct the formal analysis of queueing systems. To this aim, we present the higher-order-logic formalization of the Poisson process which is the foremost step to model queueing systems. We also verify some of its classical properties. Moreover, we used the formalization of the Poisson process to model and verify the error probability of a generic optical communication system. Then we present the formalization of Continuous-Time Markov Chains along with the Birth-Death process. Lastly, we demonstrate the utilization of our developed infrastructure by presenting the formalization of an M/M/1 queue which is widely used to model telecommunication systems. We also formally verified the generic result about the average waiting time for any given queue and applied it on an airport runway model.

Thesis

• Formalization of Continuous Time Markov Chains with Applications in Queuing Theory

HOL Script

Formalization and Applications

• Download