Sound Dynamic Fault Trees Analysis using HOL Theorem Proving
Abstract
Dynamic Fault Trees (DFTs) are increasingly being used for modeling the failure behavior of systems, particularly dynamic behaviors that cannot be captured using conventional combinatorial models. Traditionally, paper and pencil and simulation are used for the analysis of DFTs. While the former can provide generic expressions for the probability of failure, its results are prone to human errors. The latter method is based on sampling and the results are not guaranteed to be complete. Leveraging upon the expressive and sound nature of higher-order logic (HOL) theorem proving, it has been recently proposed for the analysis of DFTs algebraically. In this paper, we propose a complete methodology for the formal analysis of DFTs while capturing both the qualitative and probabilistic aspects using theorem proving. In particular, this paper provides a complete formalization for DFT gates and their corresponding simplifications properties based on the algebraic approach, as well as the formalized probabilistic behavior of the DFT gates. To demonstrate the utilization of our methodology, we apply it for the formal analysis of two safety-critical systems, namely: a drive-by-wire system and a cardiac assist system.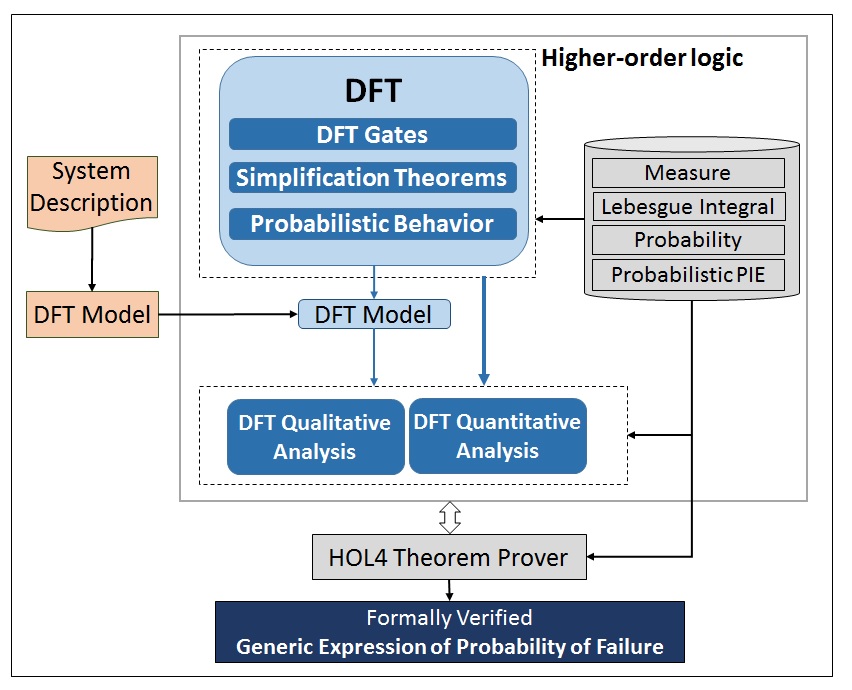
HOL Scripts
DFT Theories (PDF format)


