· A. Gawanmeh: “Theorem Proving based Framework for Verification of Group Key Protocols”; In: O. Ait Mohammed, C. Munoz and S. Tahar (Eds.) International Conference on Theorem Proving in Higher-Order Logics (TPHOLs'08), Emerging Trend Proceedings, Montreal, QC, Canada, August 2008, pp. 9-20.

· A. Gawanmeh, L. J. Ben Ayed., and S. Tahar: “Event-B based Invariant Checking of Secrecy in Group Key Protocols”; In Proc. IEEE LCN Workshop on Network Security (WNS'08), Montreal, Quebec, Canada, October 2008, pp. 950-957, IEEE Computer Society Press.

· A. Gawanmeh and S. Tahar: “Rank Theorems for Forward Secrecy in Group Key Management Protocols”; In Proc. IEEE International Conference on Advanced Information Networking and Applications Workshops (AINAW'07), Niagara Falls, Canada, May 2007, pp. 18-23. IEEE Computer Society Press.

· A. Gawanmeh, L. Jemni Ben Ayed and Sofiene Tahar: “Verification of Forward Secrecy for Group Key Protocols in Event-B Refinement”. Technical Report, Concordia University, Department of Electrical and Computer Engineering, October 2008. [28 pages]

· A. Gawanmeh, L. Jemni Ben Ayed and Sofiene Tahar: “Modeling and Verification of a Tree-based GDH protocol in Event B”. Technical Report,  Concordia University, Department of Electrical and Computer Engineering,  October 2008. [20 pages]

· A. Gawanmeh, A. Bouhoula and Sofiene Tahar: “Rank Functions based Inference System for Group Key Management Protocols Verification”. Technical Report, Concordia University, Department of Electrical and Computer Engineering, March 2007.[26 pages]

· A. Gawanmeh and Sofiene Tahar: “Rank Theorems for Forward Secrecy in Group Key Management Protocols”. Technical Report, Concordia University, Department of Electrical and Computer Engineering, December 2006. [23 pages]

· A. Gawanmeh and Sofiene Tahar: “Formal Specification Requirements for Group Key Management Protocols”. Technical Report, Concordia University, Department of Electrical and Computer Engineering, January 2006. [19 pages]

Dr. Amjad Gawanmeh

Dr. Sofiene Tahar

Dr. Adel Bouhoula

Dr. Leila Jemni

· A. Gawanmeh, A. Bouhoula, and S. Tahar: Rank Functions based Inference System for Group Key Management Protocols Verification; International Journal of Network Security, Vol. 8, No. 2, Science Publications, March 2009, pp. 187-198.

· A. Gawanmeh, “On the Formal Verification of Group Key security Protocols”. Ph.D. Department of Electrical and Computer Engineering, Concordia University, Montreal, Quebec, Canada, September 2008.

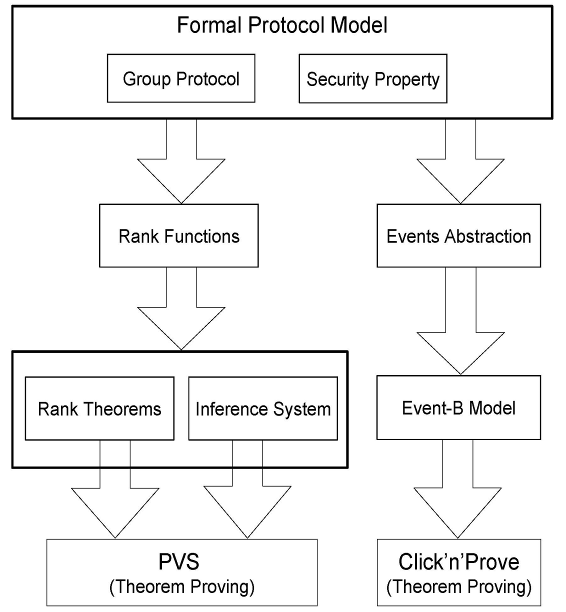
The correctness of group key security protocols in communication systems remains a great challenge because of dynamic characteristics of group key construction as we deal with an open number of group members. Therefore, verification approaches for two parties protocols cannot be applied on group key protocols. Security properties that are well defined in normal two-party protocols have different meanings and different interpretations in group key distribution protocols, and so they require a more precise definition before we look at how to verify them. An example of such properties is secrecy, which has more complex variations in group key context: forward secrecy, backward secrecy, and key independence.

In this project, we present a combination of three different theorem-proving methods to verify security properties for group-oriented protocols. We target regular group secrecy, forward secrecy, backward secrecy, and collusion properties for group key protocols. In the first method, rank theorems for forward properties are established based on a set of generic formal specification requirements for group key management and distribution protocols. Rank theorems imply the validity of the security property to be proved, and are deducted from a set of rank functions we define over the protocol. Rank theorems can only reason about absence of attacks in group key protocols. In the second method, a sound and complete inference system is provided to detect attacks in group key management protocols. The inference system provides an elegant and natural proof strategy for such protocols compared to existing approaches. It complements rank theorems by providing a method to reason about the existence of attacks in group key protocols. However, these two methods are based on interactive higher-order logic theorem proving, and therefore require expensive user interactions. Therefore, in the third method, an automation sense is added to the above techniques by using an event-B first-order theorem proving system to provide invariant checking for group key secrecy property and forward secrecy property. This is not a straightforward task, and should be based on a correct semantical link between group key protocols and event-B models. However, in this method, the number of protocol participants that can be considered is limited; it is also applicable on a single protocol event. Finally, it cannot model backward secrecy and key independence. We applied each of the developed methods on a different group protocol from the literature illustrating the features of each approach.

As future work, an interesting issue to be considered is modeling and verifying liveness security properties using event-B. In addition, an extension of the event-B based model to handle a parameterized number of participants shall be explored. It will also be interesting to investigate modeling backward secrecy and key independence using event-B. However, in order to achieve this, major modifications of the B approach are required, mainly, tool support.