The computer implementation of a majority of engineering and physical systems requires the discretization of continuous parameters (e.g., time, temperature, voltage, etc.). Such systems are then called discrete-time systems and their dynamics can be described by difference or recurrence equations. Recently, there is an increasing interest in applying formal methods in the domain of cyber-physical systems to identify subtle but critical design bugs, which can lead to critical failures and monetary loss. In this paper, we propose to formally reason about discrete-time systems using the z-Transform, which is a mathematical tool to transform a time-domain model to a corresponding complex-frequency domain model. In particular, we present the HOL Light formalization of the z-Transform and difference equations along with some important properties such as linearity, time-delay and complex translation. An interesting part of our work is the formal proof of the uniqueness of the z-Transform. Indeed, the uniqueness of the z-Transform plays a vital role in reliably deducing important properties of complex systems. We apply our work to formally analyze a switched-capacitor interleaved DC-DC voltage doubler and an infinite impulse response (IIR) filter, which are important components of a wide class of power electronics, control and signal processing systems.

Applications

Switched-Capacitor (SC) Power Converter

The ncreased density of integrated chips resulted in high power dissipation which is known as energy crisis in VLSI industry. In order to overcome this issue, power management techniques can be applied at the system, circuit or device level depending on the system complexity and nature of the device operation. DC-DC converters are one of the most important circuit level power management modules which convert an unregulated input DC voltage into an output voltage that is regulated at a given reference value for varying line and output loading conditions. Mainly, integrated DC-DC converters can be divided into three classes namely linear regulators, switch mode power converters and switched-capacitor power converters. In this paper, we aim at formal modeling and analysis of switched-capacitor (SC) DC-DC converters due to their robustness and wide application domain.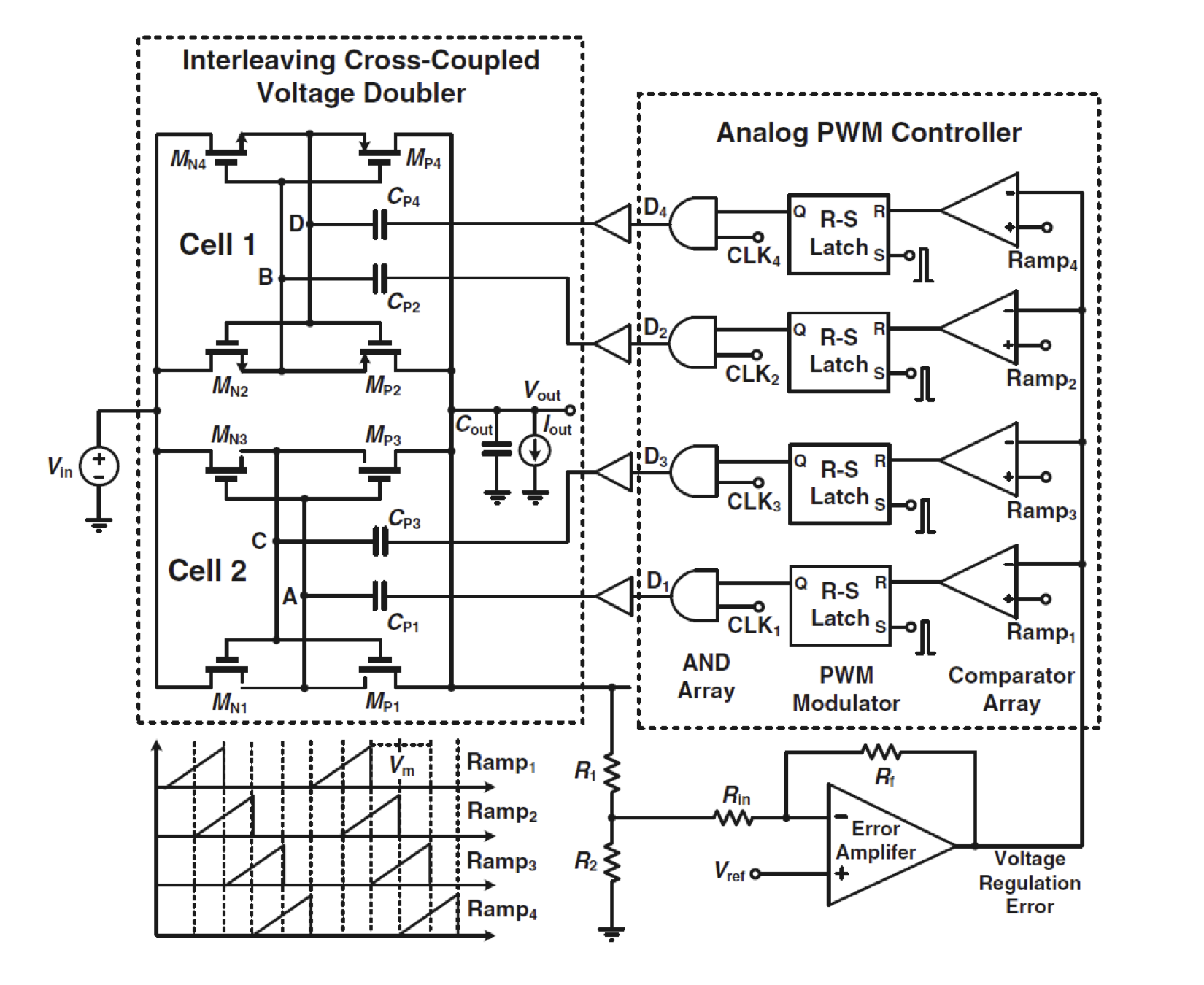

Infinite Impulse Response (IIR) Filter

Digital filters are fundamental components of almost all signal processing and communication systems. An impulse response of a system describes its behaviour under an external change (mathematically, this describes the system response when the dirac-delta function is applied as an input). Infinite impulse response (IIR) filters have an impulse response function which is non-zero over an infinite length of time. Given the filter specifications in terms of frequency response, the first step is to model the filter using constant coefficient difference equations. The next step is to express it in the form of transfer function using the Z-transform properties. Consequently, frequency response analysis and architectural optimization can be performed based on the given specifications. https://hvg.ece.concordia.ca/Publications/Journals/JAL18.pdf

Publications

1. U. Siddique, M. Y. Mahmoud and S. Tahar: Formal Analysis of Discrete-Time Systems using z-Transform, Journal of Applied Logic, Vol. 5, No. 4, June 2018, pp. 875-906.
   
   
2. U. Siddique, M. Y. Mahmoud and S. Tahar: On the Formalization of Z-Transform in HOL, G. Klein and R. Gamboa (Eds.), Interactive Theorem Proving,Lecture Notes in Computer Science Volume 8558, 2014, pp 483-498. [Proc. Conference on Interactive Theorem Proving (ITP'14), Vienna, Austria, July 2014]
   
   

Source Code

HOL Light Sources